|

|
Assoc. Prof. Dr. Cihan Tekoğlu
Department of Mechanical Engineering
TOBB University of Economics and Technology
Söğütözü Cad. No: 43,
Söğütözü, Ankara, 06560 TURKEY
e-mail: cihantekoglu@etu.edu.tr
phone: +90 (312) 292 40 65
fax: +90 (312) 292 40 91
|

|
|
My
research interests span different areas of macro/micro mechanics of
materials, with a particular focus on metamaterials, and understanding
and improving the fracture behaviour of metals and composites. Although
my main work is devoted to theoretical and computational mechanics, I
have recently started conducting experimental studies as well. In the
following, I briefly state my expertise and give an outlook on my
future research plans.
Metamaterials
Evolutionary
optimization has led natural materials to have remarkably efficient
mechanical properties: wood has a specific strength comparable with
that of the strongest steel, the fracture toughness of bone is an order
of magnitude larger than engineering ceramics, etc. Yet, there is
nothing special about the mechanical properties of the individual
blocks, but it is the arrangement of these building blocks, i.e. the
micro-architecture, which optimizes the mechanical performance. The
ever-increasing demand for multi-functional engineering materials
forces scientists and engineers to develop novel strategies to combine
usually contradicting properties, such as high strength and high
ductility, or high stiffness and low actuation energy, in a single
material. Some topics of interest for me are:
|
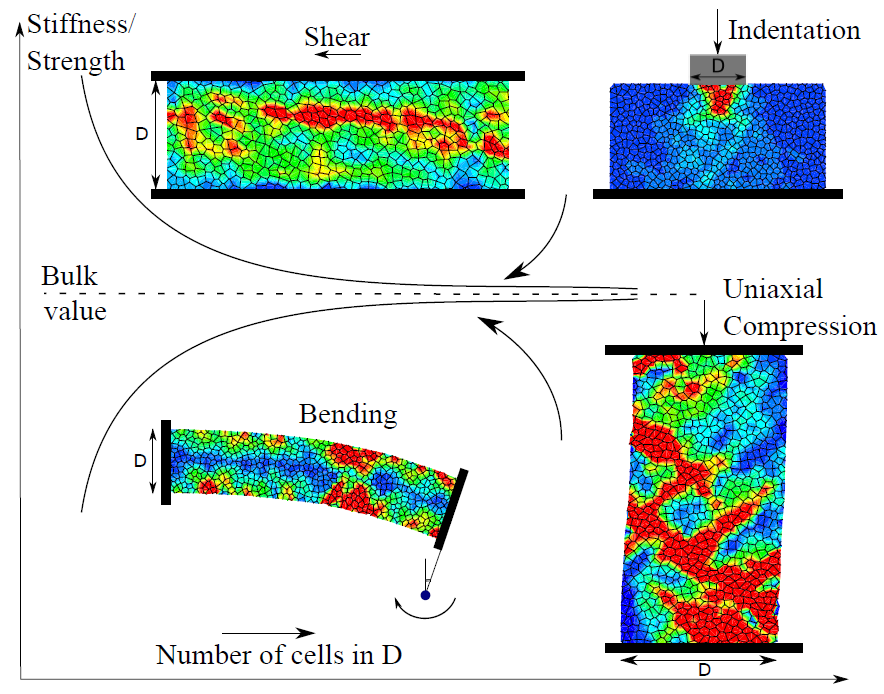
Figure 1: Size-effects
observed for 2D Voronoi microstructures under different loading
conditions. The contour plots show typical strain localization patterns
[4].
|
Cellular solids, which
are a relatively new class of engineering materials with a great
potential to be used in strong, stiff and lightweight structures.
Despite their superior bulk properties, if one of the structural
dimensions of a cellular solid has the same order of magnitude as the
cell size, the effectivemacroscopic response of the solid is dictated
by the individual excitements of the cells, which results in
size-dependent mechanical properties [1]. In order to understand the
effect of the cellular morphology on the mechanical behaviour, we
performed finite element (FE) calculations on model materials [2, 3,
4], see e.g. Fig. 1. By comparing the results with generalized
continuum theories, which incorporate a length scale to capture size
effects, we critically assessed the capabilities of different theories
in the elastic deformation range. The best agreement is obtained for
the strain divergence theory that we proposed, where the divergence of
strain is taken as an additional deformation measure [3].
|
|
Design of multi-functional materials, which combine mechanical functions (such as stiffness and strength) witho ther
properties (such as thermal or electrical conductivity, shape changing
capability, etc.). Recent studies have shown that some lattice
materials (e.g. two-dimensional (2D) Kagome structure and its 3D
equivalent [5]) have a great potential to be used in multi-functional
applications: if one of the lattice elements (i.e. beams or rods) is
replaced with an actuator, the material can undergo large shape changes
when the actuator is deployed, while it provides stiffness against
external loads when the actuator is not triggered. The Kagome lattice
is a member of the family of semi-regular tessellations of the plane.
Two fundamental questions naturally arise: i-) What makes a lattice
material suitable for actuation? ii-) Are there other tessellations
more effective than the Kagome lattice for actuation? In order to
answer these questions, we first established a set of topological
criteria to identify micro-architectures suitable for actuation [6],
and determined the sufficient symmetry conditions for isotropy of
elastic moduli [7]. We then contrived four novel 2D in-plane isotropic
lattice materials in light of these criteria [8], see Fig. 2. One of
the proposed designs (the Double Kagome lattice, see Fig.
2c) is found to match the optimal elastic properties of the Kagome
structure, while it requires less energy for (single member) actuation.
The only downside of the DK lattice appears to be that the displacement
field induced by actuation attenuates faster than in a Kagome lattice,
meaning that the DK lattice has a lower shape changing capacity.
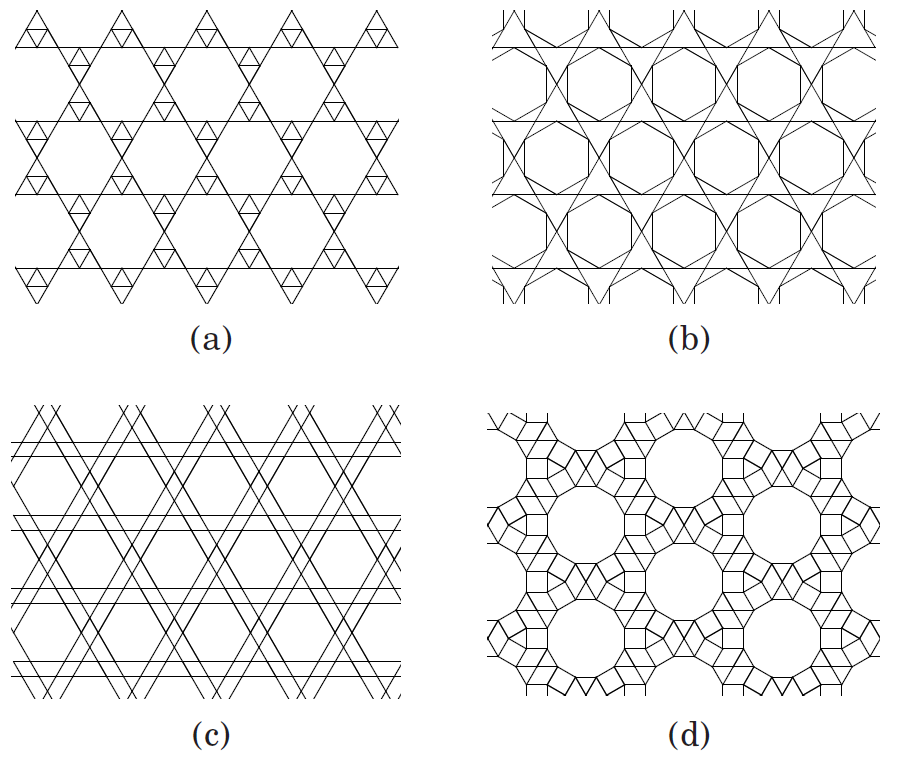
Figure 2: The
four newly contrived 2D lattice materials: (a) Kagome with concentric
triangles (KT), (b) Kagome with concentric hexagons (KH), (c) Double
Kagome (DK), and (d) the Modified Dodecagonal structure (MD).
|
My quest for stiff/strong shape-morphing lattice materials progresses
with fruitful outcomes. Recently, I designed two different families of
2D in-plane isotropic lattice materials, and some members of both
families turned out to possess a negative Poisson ratio (NPR). Owing
the their underlying architecture, NPR materials offer attractive
mechanical properties. For example, unlike a positive Poisson ratio bar
or plate, which assumes a saddle shape when bent, NPR materials take
convex shapes that are more appropriate for sandwich panels for
aircraft or automobiles, see e.g. [9, 10]. With their high resistance
to shear and indentation, and high energy absorption capacity and
toughness, NPR materials have a large potential to be used in different
applications such as fasteners and rivets, sensors, medical
applications (e.g. artificial blood vessels), bullet-proof helmets and
vests, intelligent textiles, internal structure for adaptive airplane
wing box configurations, etc. My research group currently characterizes
the mechanical properties of the NPR materials that I designed. These
new materials cover a relatively large range of different NPR values,
and some of them
|
have higher stiffness values compared to the existing
2D NPR lattices. In the long term, I am planning to extend (some) of
these 2D lattice designs to 3D, that could for example be used in
crashworthiness applications.Ductile fracture of metals and composites
The
mechanical properties of structural metallic alloys are continually
improved such that cleavage and intergranular fracture mechanisms are
mostly successfully avoided, leaving ductile fracture as the main
failure mechanism upon overloading. Therefore, together with fatigue
and corrosion, ductile fracture is the key ingredient in structural
integrity assessment of metals. Most of the ductile fracture models in
the literature neglect the presence of second-phase particles and make
use of phenomenological stress and/or strain controlled void nucleation
laws, where the nucleation stress/strain values are defined with
respect to the overall values in the material, and not to the local
field quantities in the particles or along the particle-matrix
interfaces. If, however, the particle volume fraction is larger than
5-10 %, neglecting the presence of the particles leads to dramatically
poor estimates for the fracture strain. In order to explicitly account
for the effect of second phase particles on the ductile fracture
process, we integrated a damage model based on the
Gologanu-Leblond-Devaux (GLD) constitutive behavior with a mean-field
homogenization scheme [11]. The integrated model is able to account for
the per-phase and overall stress/strain response of the material, and,
as importantly, for the softening induced by particle fracture or
decohesion, which cannot be captured by regular Gurson type models due
to a lack of coupling between void nucleation and particle response
[12]. The proposed model is shown to successfully predict the fracture
strain of dual-phase (DP) [13]. I have successfully completed a project
funded by The Scientific and Technological Research Council of Turkey
(T¨UB˙I TAK), entitled “Microstructural optimization of dual-phase (DP)
steels”, and I am planning to extend the approach we used to study the
DP steels to a wide class of metallic alloys, such as TRIP steels and
Titanium alloys.
In
order to address the effect of crystal plasticity on growth and
coalescence of voids in single crystals, we performed a large set of FE
calculations on 3D representative unit cells containing a spherical
void. We were able to predict the onset of void coalescence by using
the Thomason criterion—which was initially developed in the framework
of isotropic perfect plasticity—within 20 % relative error for most
cases, and often more accurately [14]. A more challenging task is to
provide a constitutive damage model that can account for plastic
anisotropy. For this purpose, we coupled the Gurson model with an
anisotropic yield criterion, the Facet method, which successfully
represents the yield surfaces of both single and polycrystals, even for
sharp crystallographic textures [15].
I have also contributed
to the extension of the GLD model to account for the rotation of the
voids. We proposed a void rotation law and showed that it gives
excellent agreement with 3D unit cell calculations [16]. We have also
coupled the GLD damage model with a more realistic, Kocks-Mecking type
strain hardening law, which explicitly takes into account the two main
strain hardening stages observed in metals, referred to as stage III
and stage IV in the literature. The predictions of this extended damage
model are in very good agreement with the results of the FE voided unit
cell calculations [17]. A comprehensive summary for a part of my work
on fracture mechanics is explained in a review paper [18].
Although
there exists fairly accurate (theoretical/numerical) models for void
growth, especially for isotropic materials, proper treatments of void
nucleation and localization of plastic deformation leading to final
failure are still open research topics. An important part of my work
concerning fracture mechanics is therefore devoted to the development
ofmicroscopic localization (i.e. void coalescence) criteria
incorporating the effect of shear loads [19, 20], and the effect of the
presence of a secondary family of voids/particles [21]. I have also
worked on macroscopic plastic localization dominated failure, which led
to the important conclusion that: “At sufficiently high stress
triaxiality, a clear separation exists between the macroscopic and
microscopic modes of localization. At lower stress triaxialities,
however, the onset of macroscopic localization and coalescence occurs
simultaneously” [22]. All these studies on localized deformation gave
me the opportunity to build a robust FE framework for performing
representative volume element calculations under constant stress
triaxiality, Lode parameter, and shear ratio [23]. I have ongoing
studies on failure under low stress triaxiality, with a particular
interest on the effect of “shear ratio” on ductile fracture. An
ambitious target for me is to develop a localization model for randomly
distributed and oriented voids/particles under general loading
conditions.
Another
challenging topic in the field of ductile fracture is the effect of
volume fraction, shape, size and spatial distribution of second phase
particles on the crack propagation mechanisms. I have recently
completed a project funded by T¨UB˙ITAK, entitled “A numerical and
experimental investigation of crack propagation mechanisms in ductile
metal plates”. The main conclusion of this study was that “large
particles with a large volume fraction lead to a slanted or a cupcone
crack, while small particles with a small volume fraction lead to a
cup-cup fracture surface morphology for ductile plates teared under
mode I loading (see Fig. 3)”, which we were able
to demonstrate both in an experimental [24] and in a numerical framework [25].
 (a)
(b)
|
References[1] C. Tekoğlu, 2007. Size effects in cellular solids. PhD Thesis, University of Groningen, The Netherlands. (url)
[2] C. Tekoğlu, P. R. Onck, 2005. Size effects in the mechanical behavior of cellular materials. J. Mater. Sci. 40, 5911-5917. (url)
[3] C. Tekoğlu,
P. R. Onck, 2008. Size effects in two-dimensional Voronoi foams: A
comparison between generalized continua and discrete models. J. Mech.
Phys. Solids 56, 3541-3564. (url)
[4] C. Tekoğlu, L. G. Gibson, T. Pardoen, P. R. Onck, 2011. Size effects in foams: Experiments and modeling. Prog. Mater. Sci. 56, 109-138 (url)
[5]
N. A. Fleck, V. S. Deshpande and M. F. Ashby, 2010. Micro-architectured
materials: past, present and future. Proc. R. Soc. A. (published
online). (url)
[6] T. N. Pronk, C. Ayas, C. Tekoğlu, 2017. A quest for 2D lattice materials for actuation. J. Mech. Phys. Solids 105, 199-216. (url)
[7] C. Ayas, C. Tekoğlu, 2018. On the sufficient symmetry conditions for isotropy of elastic moduli. J. Appl. Mech. 85, 074502-074502-5. (url)
[8] W. E. D. Nelissen, C. Ayas, C. Tekoğlu, 2019. 2D lattice material architectures for actuation. J. Mech. Phys. Solids 124, 83-101. (url)
[9] S. R. Lakes, 1993. Advances in negative Poisson’s ratio materials Advanced Materials 5, 293-296. (url)
[10] S. R. Lakes, 2017. Negative-Poisson’s-Ratio Materials: Auxetic Solids Annual Review of Materials Research 47, 63-81. (url)
[11] M. Inanc, T. Pardoen, C. Tekoğlu,
2015. An Enhanced Mori-Tanaka Homogenization Scheme for Incremental,
Non-Linear Rate-Independent Plasticity. In: Proceedings of the 5th
ECCOMAS Thematic Conference on the Mechanical Response of Composites,
COMPOSITES 2015, 07-09 September, 2015, University of Bristol, UK
[CD-ROM].
[12] C. Tekoğlu, T. Pardoen, 2010. A micromechanics based damage model for composite materials. Int. J. Plasticity 26, 549-569. (url)
[13] A. P. Pierman, C. Tekoğlu,
T. Pardoen, P. J. Jacques, 2009. Nucleation, growth and coalescence of
voids in dual phase steels: from model microstructures to
microstructure based modeling. In: Proceedings of the 12’th
International Conference on Fracture, Ottawa, Canada [CD-ROM].
[14] S. K. Yerra, C. Tekoğlu,
F. Scheyvaerts, L. Delannay, P. Van Houtte, T. Pardoen, 2010. Void
growth and coalescence in single crystals. Int. J. Solids Structures
47, 1016-1029. (url)
[15] S. K. Yerra, C. Tekoğlu,
A. Van Bael, L. Delannay, P. Van Houtte, T. Pardoen, 2010. The
Facet-Gurson model for ductile damage process. In: 18’th European
Conference on Fracture, August 30 - September 03, 2010, Dresden,
Germany, [CD-ROM].
[16] F. Scheyvaerts, P. R. Onck, C. Tekoğlu,
T. Pardoen, 2011. The growth and coalescence of ellipsoidal voids in
plane strain under combined shear and tension. J. Mech. Phys. Solids
59, 373-397 (url)
[17] L. Lecarme, C. Tekoğlu,
T. Pardoen, 2011. Void growth and coalescence in ductile solids with
stage III and stage IV strain hardening. Int. J. Plasticity 27,
1203-1223. (url)
[18] T. Pardoen, F. Scheyvaerts, A.Simlar, C. Tekoğlu, P. R. Onck, 2010. Multiscale modeling of ductile failure in metallic alloys. C. R. Physique 11, 326-345. (url)
[19] C. Tekoğlu,
J.-B. Leblond, T. Pardoen, 2012. A criterion for the onset of void
coalescence under combined shear and tension. J. Mech. Phys. Solids 60,
1363-1381. (url)
[20] M.E. Torki, C. Tekoğlu,
J.-B. Leblond, A.A. Benzerga, 2017. Theoretical and numerical analysis
of void coalescence in porous ductile solids under arbitrary loadings.
Int. J. Plasticity 91, 160-181. (url)
[21] C. Tekoğlu, 2015. Void coalescence in ductile solids containing two populations of voids. Eng. Fract. Mech. 147, 418-430. (url)
[22] C. Tekoğlu,
J.W. Hutchinson, T. Pardoen, 2015. On localization and void coalescence
as a precursor to ductile fracture. Philos. T. R. Soc. A. 373, 1-9. (url)
[23] C. Tekoğlu,
2014. Representative volume element calculations under constant stress
triaxiality, Lode parameter, and shear ratio. Int. J. Solids Struct.
51, 4544–4553. (url)
[24] C. Tekoğlu,
S¸ . C¸ elik, H. Duran,M. Efe, K. L. Neilsen, submitted. Experimental
Investigation of Crack Propagation Mechanisms in Commercially Pure
Aluminium Plates. To: Proceedings of 1st International Workshop on
Plasticity, Damage and Fracture of Engineering Materials (IWPDF2019),
August 22-23, 2019, Ankara, Turkey.
[25] C. Tekoğlu,
K. L. Nielsen, 2019. Effect of damage-related microstructural
parameters on plate tearing at steady state. Eur. J. Mech. A-Solid.
Advance online publication. (url)
|
|